Welcome to our blog post on orthogonal vectors! In mathematics, vectors play a crucial role in various fields, including physics, computer science, and engineering. Understanding the concept of orthogonal vectors is fundamental in many applications, so let’s dive in and explore this topic together.
1. Definition of Vectors
Before we delve into orthogonal vectors, let’s first clarify what vectors are. In mathematics, a vector is a quantity that has both magnitude and direction. It is often represented by an arrow, where the length of the arrow corresponds to the vector’s magnitude, and the direction it points in represents its orientation.
2. Orthogonal Vectors Explained
Orthogonal vectors, also known as perpendicular vectors, are a special case of vectors. Two vectors are considered orthogonal if they are perpendicular to each other. This means that when the vectors are placed tail-to-tail, they form a right angle between them.
3. Geometric Interpretation
Geometrically, orthogonal vectors can be visualized as two arrows pointing in different directions that intersect at a right angle. For example, consider a vector representing the direction east and another vector representing the direction north. These vectors are orthogonal since east and north are perpendicular directions.
4. Dot Product and Orthogonality
The dot product is a mathematical operation between two vectors that yields a scalar value. One of the key properties of the dot product is that if the dot product of two vectors is zero, then the vectors are orthogonal. This property allows us to determine whether two vectors are orthogonal by calculating their dot product.
5. Applications of Orthogonal Vectors
Orthogonal vectors have numerous practical applications. In physics, they are used to analyze forces acting on objects in different directions. In computer science, orthogonal vectors are employed in algorithms for image processing, computer graphics, and machine learning. They also play a significant role in linear algebra, which is the foundation of many mathematical concepts.
Conclusion
Understanding orthogonal vectors is essential in various mathematical fields and real-world applications. We’ve explored the definition of vectors, the concept of orthogonal vectors, their geometric interpretation, the role of dot products in determining orthogonality, and some practical applications. Feel free to leave a comment below and let us know how you’ve encountered orthogonal vectors in your studies or work!
Leave a Comment
galois theory – How to find orthogonal vectors in GF(2) – Mathematics …
Jul 2, 2015 … The space V=GF(2)n, n even, has certain subspaces W of dimension n such that all the vectors in W are orthogonal to all the vectors in V ( … – math.stackexchange.com

linear algebra – two orthogonal vectors that are not linearly …
Nov 24, 2016 … 1 Answer 1 … Yep! The vector 0 is orthogonal to all vectors and linearly dependent with all vectors. … is (1,1) and (0,0) are two orthogonal … – math.stackexchange.com

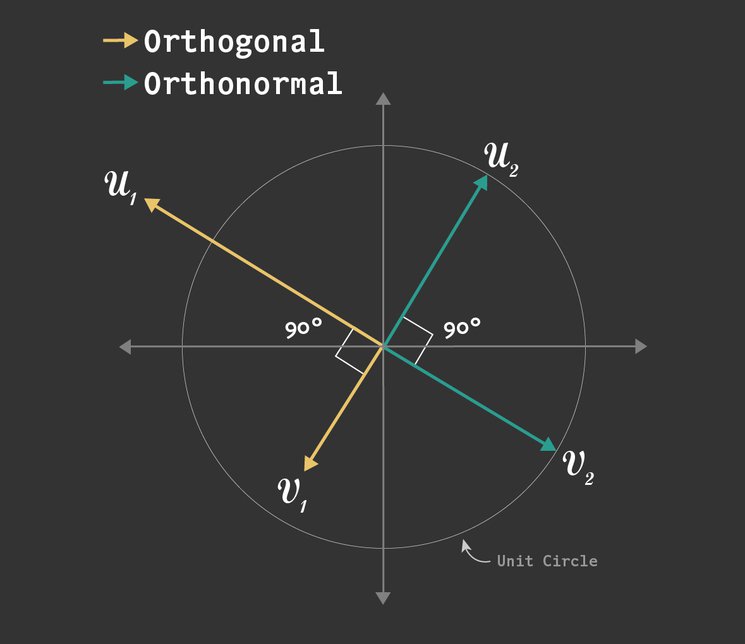
6.3 Orthogonal and orthonormal vectors
Definition. We say that 2 vectors are orthogonal if they are perpendicular to each other. i.e. the dot product of the two vectors is zero. Definition. – www.ucl.ac.uk
fa.functional analysis – Almost orthogonal vectors – MathOverflow
May 16, 2010 … Almost orthogonal vectors … This is to do with high dimensional geometry, which I’m always useless with. Suppose we have some large integer n … – mathoverflow.net

Why is the dot product of orthogonal vectors zero? | by Ms Aerin …
Mar 31, 2019 … Why is the dot product of orthogonal vectors zero? … The answer is simple. It is “by definition”. Two non-zero vectors are said to be orthogonal … – medium.com
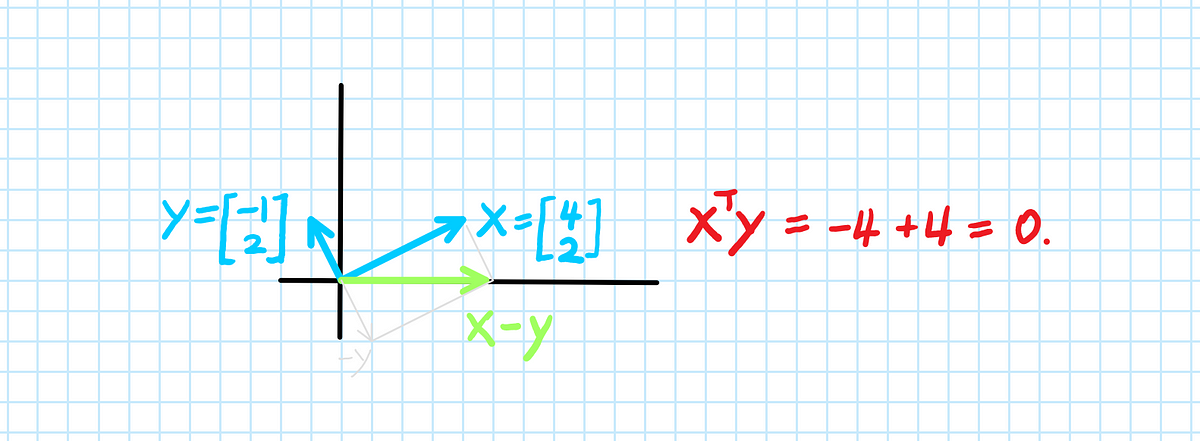
Orthogonal and Orthonormal Vectors – LearnDataSci
Two vectors u and v are considered to be orthogonal when the angle between them is 90 ∘ . In other words, orthogonal vectors are perpendicular to each other. – www.learndatasci.com
Determine If Vectors Are Orthogonal Calculator
Determine If Vectors Are Orthogonal Calculator Vectors play a fundamental role in various fields of mathematics and physics providing a powerful tool for representing quantities with both magnitude and direction. In vector analysis determining whether two vectors are orthogonal can be crucial for so – drawspaces.com

Parallel And Orthogonal Vectors Calculator
Parallel And Orthogonal Vectors Calculator: Exploring Vector Relationships Introduction In the realm of mathematics and physics vectors play a crucial role in representing quantities that have both magnitude and direction. Understanding the relationships between vectors is essential for solving vari – drawspaces.com

Check If Vectors Are Orthogonal Calculator
Check If Vectors Are Orthogonal Calculator Orthogonality is a fundamental concept in mathematics particularly in linear algebra. Vectors play a crucial role in this field and determining whether two vectors are orthogonal or not can have significant implications in various applications such as physi – drawspaces.com

Orthogonal Vectors Overview, Formula & Examples – Video …
For example, let u = ⟨ a , b ⟩ We wish to find a vector orthogonal to u , i.e. a vector v = ⟨ x , y ⟩ such that u ⋅ v = 0 ⟹ ⟨ a , b ⟩ ⋅ ⟨ x , y ⟩ = 0 … – study.com

Determine Whether The Set Of Vectors Is Orthogonal Calculator
Determine Whether The Set Of Vectors Is Orthogonal Calculator In linear algebra the concept of orthogonality plays a crucial role in various applications. The ability to determine whether a set of vectors is orthogonal or not is essential in vector analysis geometry and many other mathematical field – drawspaces.com

Dot Products and Orthogonality
Two vectors x , y in R n are orthogonal or perpendicular if x · y = 0. Notation: x ⊥ y means x · y = 0. Since 0 · x = 0 for any vector x , the zero vector is … – textbooks.math.gatech.edu