Welcome to our blog post about angle relationships! Understanding angles and their relationships is essential in various areas, including mathematics, geometry, and even everyday life. In this post, we will explore and discuss several types of angle relationships, providing examples and explanations along the way. So, let’s dive in!
Adjacent Angles
Adjacent angles are two angles that share a common vertex and a common side, but do not overlap. They are side-by-side, and their interiors do not intersect. The sum of adjacent angles always forms a straight line, which measures 180 degrees. For example, in the image below, angle A and angle B are adjacent angles, and their sum is equal to 180 degrees.

Complementary Angles
Complementary angles are two angles whose measures sum up to 90 degrees. In other words, when you add the measures of two complementary angles, the result is always 90 degrees. For instance, if angle C measures 30 degrees, then angle D would be its complementary angle, measuring 60 degrees, as shown in the diagram below.

Supplementary Angles
Supplementary angles are two angles whose measures sum up to 180 degrees. When you add the measures of two supplementary angles, the result is always 180 degrees. As an example, if angle E measures 120 degrees, then angle F would be its supplementary angle, measuring 60 degrees, as depicted in the following illustration.

Vertical Angles
Vertical angles are a pair of opposite angles formed by two intersecting lines. They share the same vertex but lie across from each other. Vertical angles are always congruent, meaning they have the same measure. In the image below, angles G and H are vertical angles, and their measures are equal.

Linear Pair Angles
Linear pair angles are adjacent angles that form a straight line when combined. Therefore, their measures sum up to 180 degrees. In other words, if two angles are adjacent and their measures add up to 180 degrees, they form a linear pair. In the illustration below, angles I and J are adjacent and form a linear pair.

Conclusion
Understanding the different types of angle relationships is crucial in various mathematical and real-life scenarios. Whether it’s determining the measurements of angles in geometry problems or comprehending the angles created by intersecting lines, knowing these relationships enhances our ability to analyze and solve problems accurately. We hope this blog post has provided you with valuable insights into the various types of angle relationships.
Now, we would love to hear from you! Do you have any questions or additional examples of angle relationships you’d like to share? Leave a comment below and let’s continue the discussion!
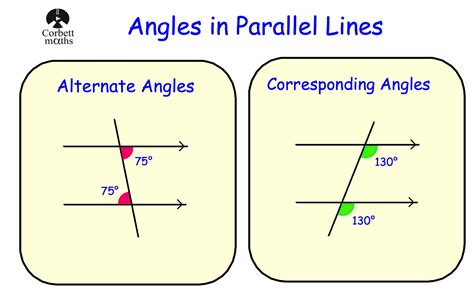
Types of Angle Relationships – Corresponding, Alternate Interior …
Jan 11, 2023 … For example, when two lines or line segments intersect, they form two pairs of vertical angles. When two parallel lines are intersected by a … – tutors.com

Angle Relationships | Overview & Types – Video & Lesson Transcript …
When the two lines intersected by the transversal are parallel, corresponding angles are congruent, alternate interior angles are congruent, alternate exterior … – study.com

Angles Types + Angle Relationships Bundle
Angle Types + Angle Relationships These angle posters and student activity provides the learner with examples and definitions of the full range of angle … – giftedandtalentedteacher.com
Transversal Of Parallel Lines Find Angle Measures Calculator
Transversal Of Parallel Lines Find Angle Measures Calculator Welcome to our comprehensive blog post on the topic of finding angle measures using a transversal of parallel lines calculator. Understanding the concept of transversals and parallel lines is crucial in geometry and this calculator will he – drawspaces.com

Angle Relationships Calculator
Angles play a crucial role in geometry and trigonometry and understanding their relationships is fundamental to solving various mathematical problems. Whether you’re a student struggling with geometry homework or a professional working with angles regularly having a reliable tool to determine angle – drawspaces.com
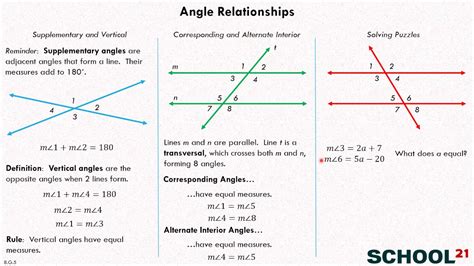
Line And Angle Relationships Calculator
Line And Angle Relationships Calculator In the world of mathematics understanding line and angle relationships is crucial. These relationships not only help us solve complex problems but also play a fundamental role in various disciplines such as engineering architecture and physics. However calcula – drawspaces.com
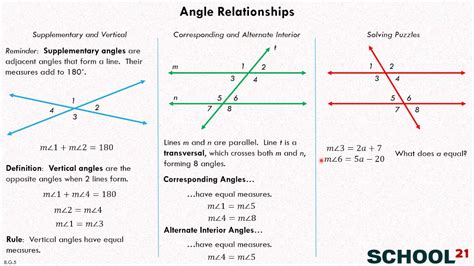
Angle Relationships With Parallel Lines Calculator
Angle Relationships With Parallel Lines Calculator Understanding angle relationships with parallel lines is an essential aspect of geometry. However calculating these angles manually can be time-consuming and prone to errors. Fortunately with the help of modern technology we now have access to angle – drawspaces.com